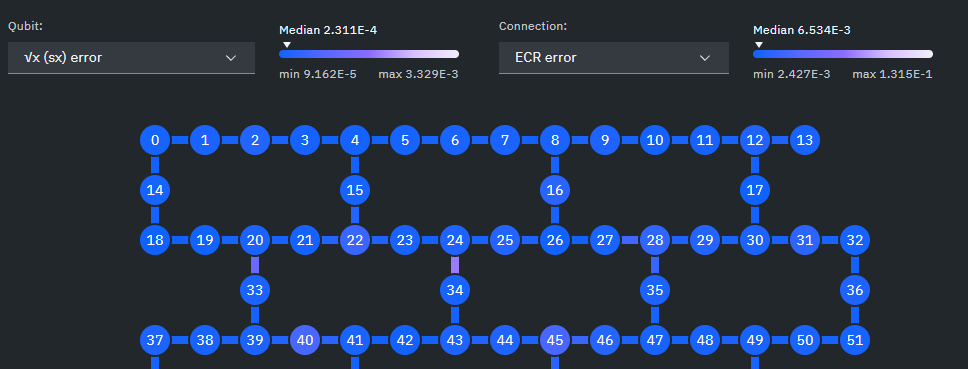
Fault-tolerance by construction
Aleks Kissinger
PsiQuantum/USyd Fault-tolerance seminar, 2025

...with the ZX-calculus of course
ZX := a handy tool for working with quantum
computations using graph rewriting
 |
 |
 |
| Optimisation | Simulation & Verification | Error Correction |
Optimising circuits the old-fashioned way
A better idea: decompose a circuit into a ZX diagram
ZX diagrams
- Gates are represented using more basic building blocks, called spiders:
$:=$ $\ \ |0...0\rangle\langle 0...0| + e^{i \alpha} |1...1\rangle\langle 1...1|$ $:=$ $\ \ |{+}...{+}\rangle\langle {+}...{+}| + e^{i \alpha} |{-}...{-}\rangle\langle {-}...{-}|$ - E.g.
$\textit{CNOT} :=$
$\sqrt{X} :=$
$Z_\alpha :=$
- Wire order doesn't matter $\Rightarrow$ treat ZX-diagrams as undirected graphs
...then use the ZX calculus
A complete set of equations for qubit QC
Clifford ZX calculus
A complete set of equations for qubit Clifford QC
efficient synthesis, equality checking, classical simulation, ...
$\approx$ "graphical stabiliser theory"
PyZX
- Open source Python library for circuit optimisation, experimentation, and education using ZX-calculus
https://github.com/zxcalc/pyzx
QuiZX


- Large scale circuit optimisation and classical simulation library for ZX-calculus
https://github.com/zxcalc/quizx
ZXLive
- GUI tool based on PyZX
https://github.com/zxcalc/zxlive
Quantum errors
- Classical error rate $\approx 10^{-18}$
- Quantum error rate $10^{-2} - 10^{-5}$
- decoherence, thermal noise, crosstalk, cosmic rays, ...
- Probability of a successful (interesting) computation $\approx 0$
Quantum error correction
into a bigger space of physical qubits:
- $E$ (or just $\textrm{Im}(E)$) defines a quantum error correcting code
- Fault-tolerant quantum computing (FTQC) requires methods for:
- encoding/decoding logical states and measurements
- measuring physical qubits to detect/correct errors
- doing fault-tolerant computations on encoded qubits
Let's see how this works...using ZX
Quantum Gates
$CNOT =$
$CZ =$
$H =$
$:=$
$R_Z[\alpha] =$
$R_X[\alpha] =$
Quantum Measurements
$|k\rangle\langle k| \propto$
...collapse the quantum state to a fixed one,
depending on the outcome $k \in \{0,1\}$:
Multi-qubit measurements
$k = 0$
$\Rightarrow$
$+1$ eigenspace of $Z \otimes \ldots \otimes Z$
$k = 1$
$\Rightarrow$
$-1$ eigenspace of $Z \otimes \ldots \otimes Z$
$\propto$
Multi-qubit measurements
Any other multi-qubit measurement can be obtained by conjugating with local Cliffords, e.g.
Modelling errors
Pauli errors are modelled by introducing X, Y, or Z
flips on edges in a ZX-diagram:
Modelling errors
Anti-commuting errors flip measurement outcomes:
Example: GHZ code
Example: GHZ code
Example: GHZ code
giving an error syndrome.
Graphical encoders
...give us a simple dictionary between QEC codes and ZX-diagrams, e.g. the GHZ code can be fully represented as:
Example: Steane code
Example: Surface code
Example: [[8, 3, 2]] Colour code
Encoders
For any CSS code, we can compute the graphical encoder from stabilisers and logicals. This computation is efficient and easy.
AK. "Phase free ZX diagrams are CSS Codes (...or how to graphically grok the surface code)". arXiv:2204.14038
For any stabiliser code, this computation is still efficient,
but it takes a bit more work.
Khesin, Lu, Shor: arXiv:2301.02356 | Khesin & Li: arXiv:2406.12083
Fault-tolerant computation
But codes are only half the story in FTQC. We also need to know how to implement operations fault-tolerantly.
How can we implement this?
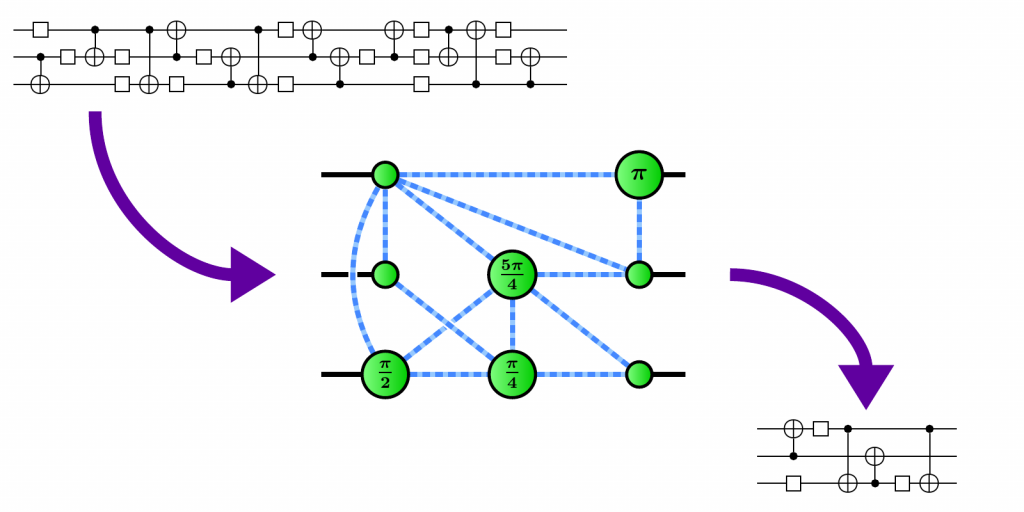
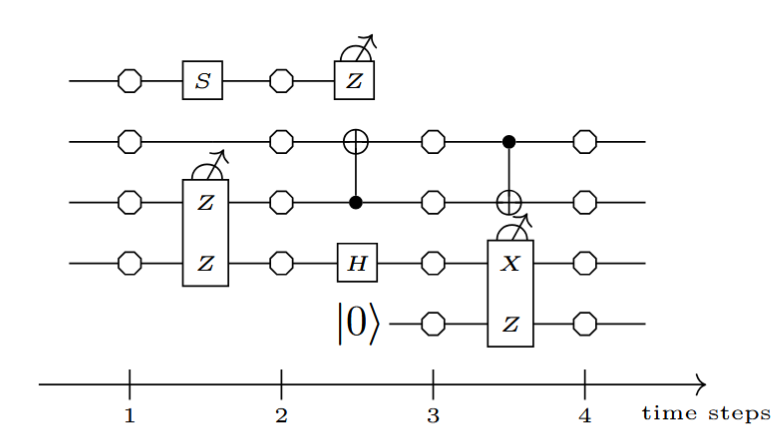
Example: measurement circuits
ZX can give us an answer:
Q: Is the LHS really equivalent to the RHS?
A: It depends on what "equivalent" means.
Example: measurement circuits
They both give the same linear map, i.e. the behave the same in the absence of errors.
But they behave differently in the presence of errors, e.g.
Solution: Fault equivalence
What we need is a notion of equivalence that captures the behaviour of circuits (or ZX-diagrams) in the presence of errors, fault-equivalence:
$D \ \hat{=}\ E$
$D\ \hat{=}\ E \implies D = E$
$D = E \ \ \not\!\!\!\implies D\ \hat{=}\ E$
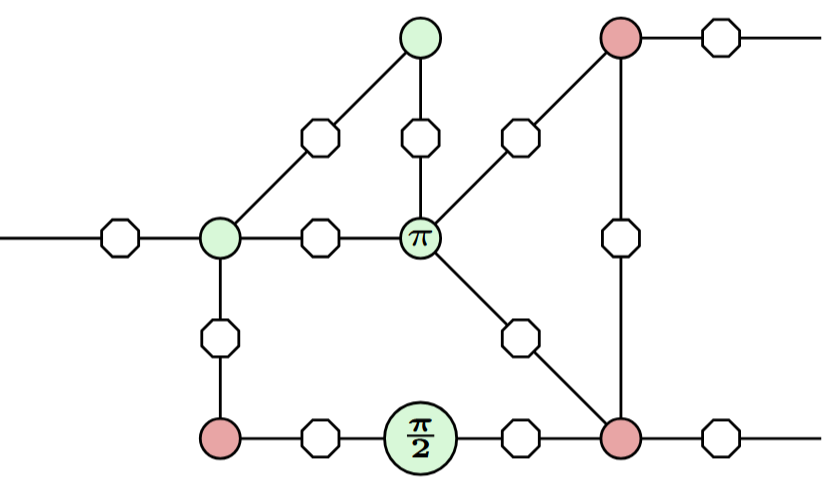
Error locations
Similar to space-time codes, we can model faults by tracking their locations in a circuit or ZX-diagram.
we allow them at any edge in the diagram:
Pauli error models
- For a circuit/diagram with a set $\mathcal L$ of fault locations, a fault is a Pauli
$F \in \mathcal P^{|\mathcal L|}$
- A Pauli error model is a choice of basic faults $F_1, \ldots, F_b$. The weight of a fault is the number of basic faults in its product.
- Ex: Phenominological/naive model:
basic faults $:=$ all single-qubit Paulis
- Ex: Circuit-level noise model:
basic faults $:=$ all single-qubit Paulis (memory errors) +
some multi-qubit Paulis (correlated gate/measurement errors)
Pauli error models
Ex: sub-models, where we remove some basic faults to represent components we assume are noise-free:
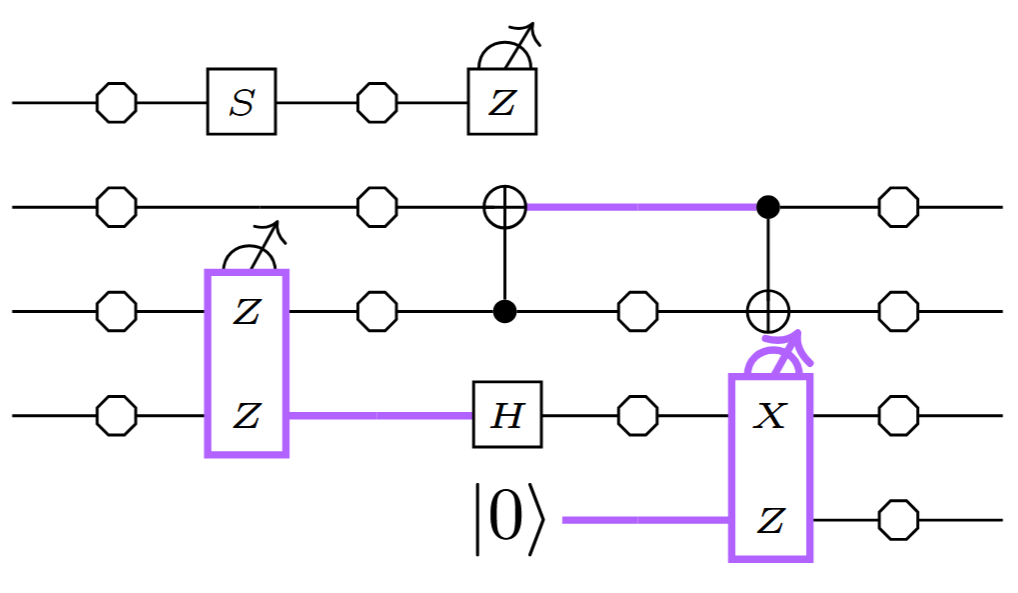
Fault-equivalence
Definition: Two circuits (or ZX-diagrams) $C, D$ are called fault-equivalent:
$C \ \hat{=}\ D$
if for any undetectable fault $F$ of weight $w$ on $C$, there exists an undetectable fault $F'$ of weight $\leq w$ on $D$ such that $C[F] = D[F']$(and vice-versa).
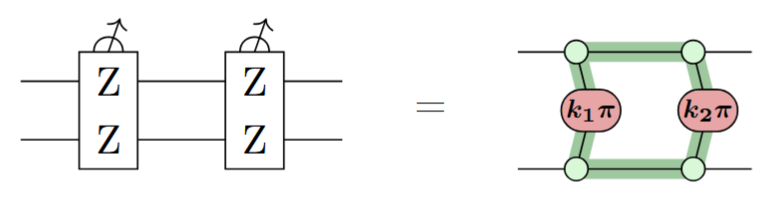
Fault-equivalence
- While all the ZX rules preserve map-equivalence, only some rules preserve fault-equivalence.
- It turns out the ones that do, e.g.
...are very useful for compiling fault-tolerant circuits!
Paradigm: Fault-tolerance by construction
Idea: start with an idealised computation (i.e. specification) and refine it with fault-equivalent rewrites until it is implementable on hardware.
Specification/refinement has been used in formal methods for classical software dev since the 1970s. Why not for FTQC?
Example: Cat state preparation
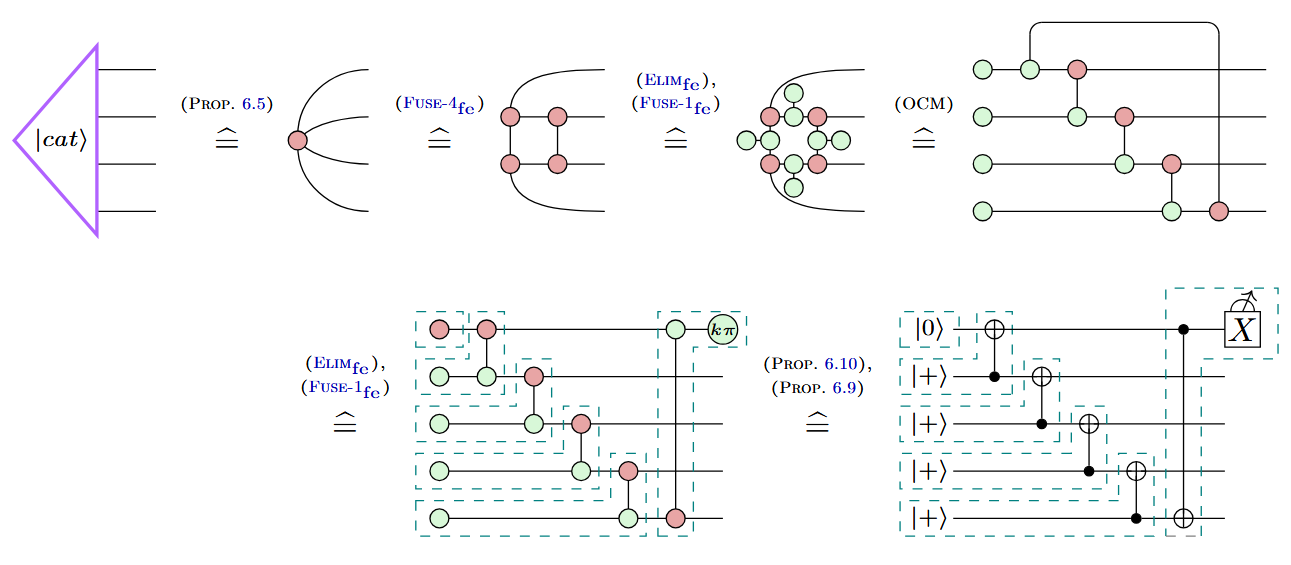
Example: Cat state preparation
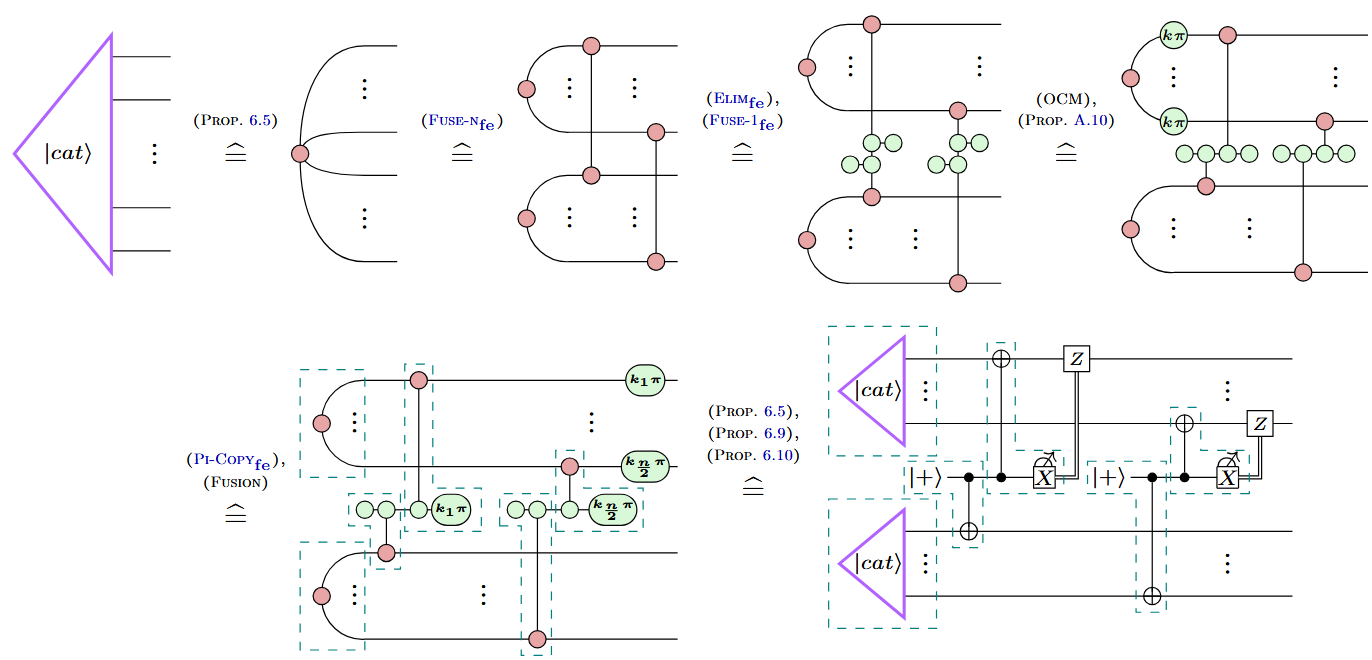
Example: Shor-style syndrome extraction
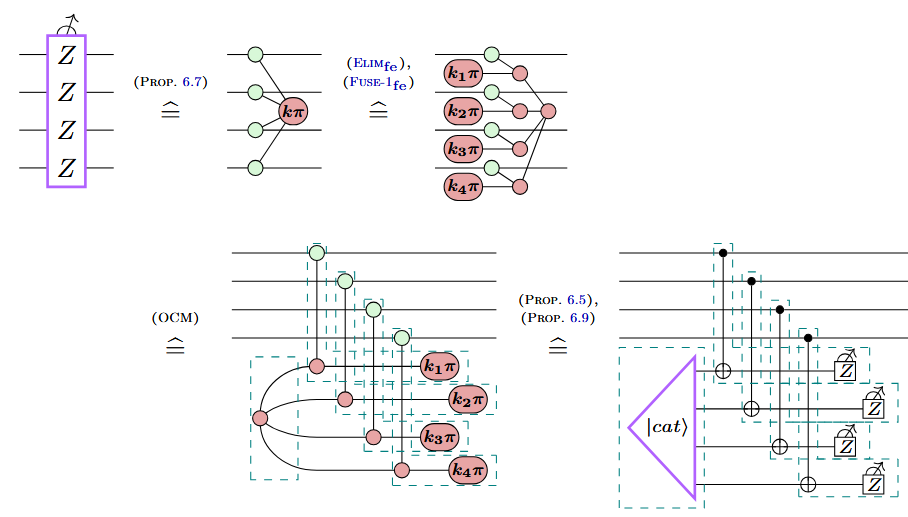
Example: A new variation on Shor

Example: Steane-style syndrome extraction
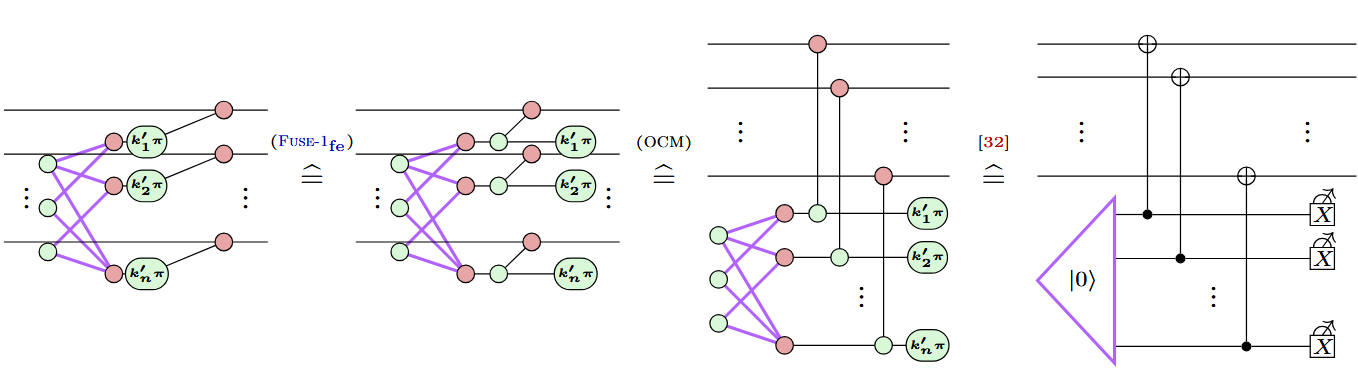
Example: A new variation on Steane (the same trick)
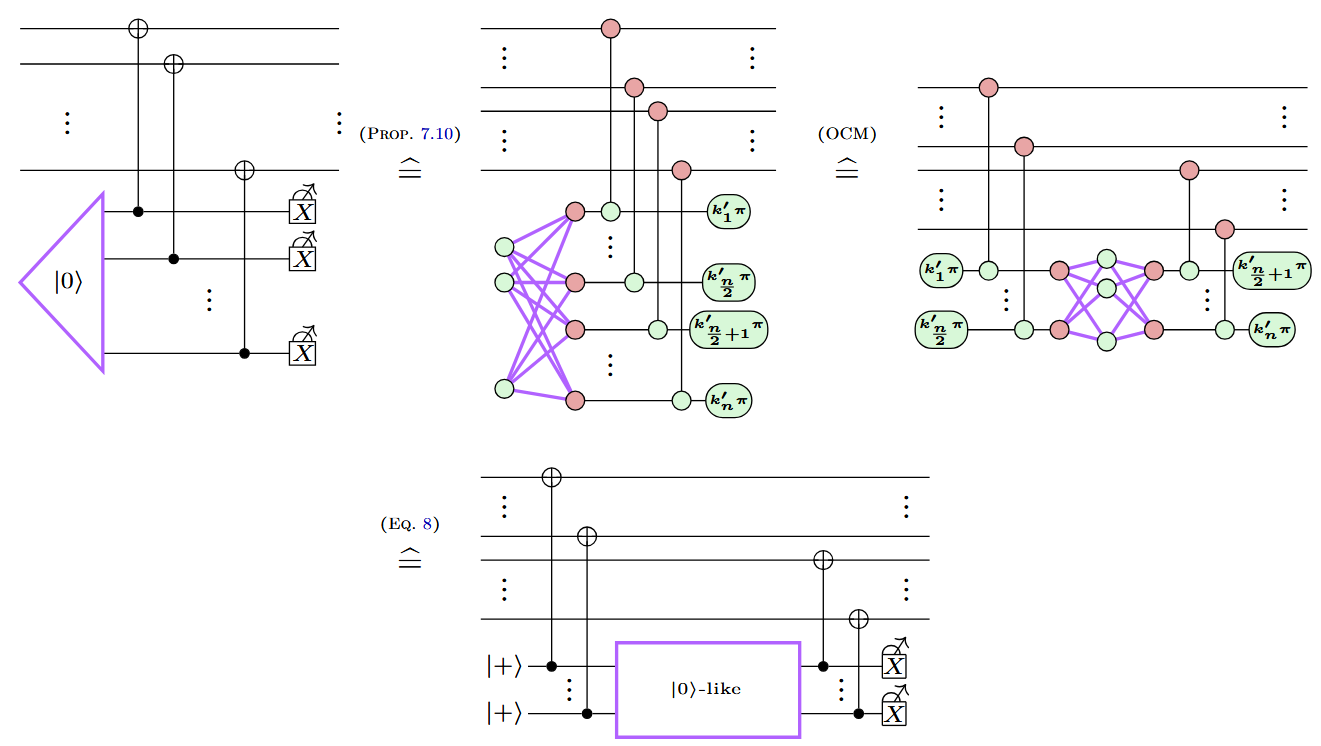
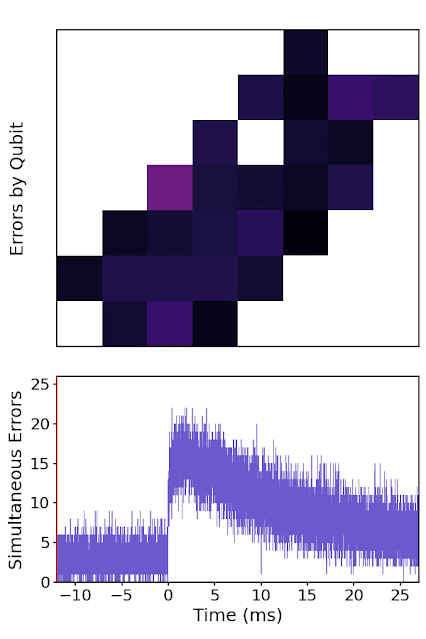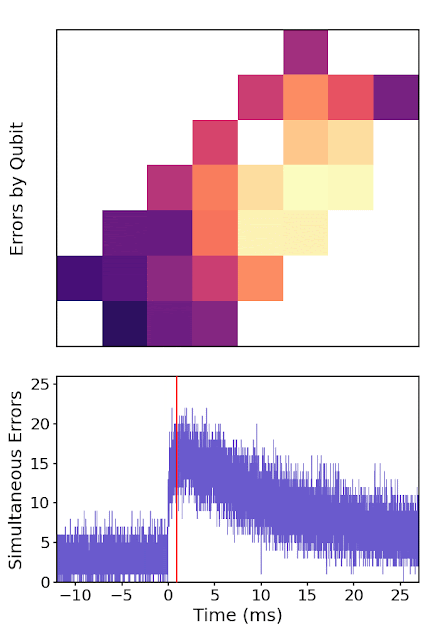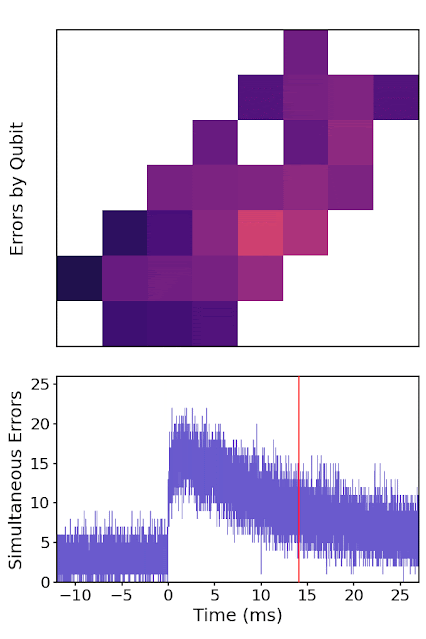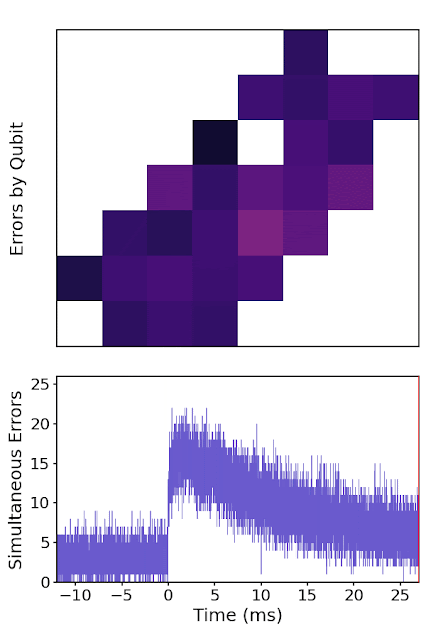
...with fewer qubits and a lower logical error rate!
Lots to do!
- A complete set of rules for fault-equivalence
(almost there!) - FT circuit optimisation
- Decoding syndromes, and preserving efficient decodability
- Bounding/relating behaviour under stochastic noise
(fault-equiv. = adversarial/worst-case noise behaviour) - Scalability
- Automation and integration (PyZX/QuiZX/Stim)
- Finding cool FT protocols, running them on hardware
"Fault Tolerance by Construction". Rodatz, Poór, Kissinger
arXiv:2506.17181

https://zxcalc.github.io/book
(free book! Ch 11 = ZX + QEC)
https://zxcalculus.com
(350 ZX papers, ~10% tagged QEC, online seminars, Discord)